Data Structure - B-Tree

Introduction

B-tree is a self-balancing tree data structure. In a B-tree each node may contain a large number of keys and children. The number of children and keys in a B-tree is defined by a single numerical parameter - order. B-tree is a generalization of 2-3-4 tree [3].

Facts about B-Tree of order K:

• Every node has at most K children.
• All leaves appear in the same level.
• A non-leaf node with K children contains K−1 keys.
• Keys in the node are ordered. Depth first in-order traversal of B-Tree produces ordered sequence of keys.
• Data lookup, insertion and deletion operations have logarithmic complexity.
• B-tree is optimized for storage systems that read and write large blocks of data.
• The number of keys in a node is often chosen such, that one node fits in one physical storage data block (4K, 65K, etc). For example: If the key size is 8 bytes, the size of child reference is 4 bytes and the storage block is 4096 bytes, then one node can have at most (4096-4)/(8+4) = 341 keys.

B-Tree of order 5 built from the array of values (7, 16, 1, 2, 5, 6, 12, 9, 21, 18) is shown below. Each node has 9 slots: 5 slots for child references and 4 slots for key values: Key slots contain either a number or when empty an underscore '_' symbol, Reference slots that have link to a child node contain '.' symbol.

Implementation

C# implementation that follows description of Comer's article ^[1] is given in two flavors:

• In-memory storage Open on github
• Persistent storage Open on github

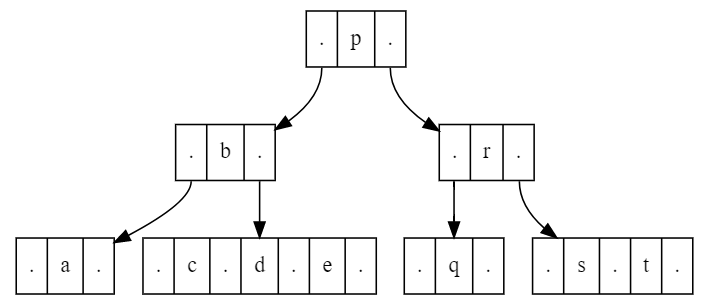
Python implementation of 2-3-4 tree with add operation as described in Wikipedia article ^[3]: Open on github

2-3-4 tree built from the input ['a', 'b', 'c', 'p', 'q', 'r', 's', 'd', 't', 'e'] is shown below:

Usage

• Persistent implementation of B-tree is used in PMS Full-Text search engine for storing metadata fields.

Links

• [1] Douglas Comer The Ubiquitous B-Tree
• [2] Br. David Carlson, B-Tree Tutorial
• [3] 2-3-4 tree article on Wikipedia