A method to decode Huffman codes

Huffman coding is a type of optimal prefix encoding that is used for lossless data compression. The Huffman coding algorithm takes as input the frequencies of symbols from a certain alphabet and constructs variable-length prefix codes that minimize the average length of the encoded data. It compresses data by replacing each fixed-length input symbol with the corresponding variable-length prefix-free output code. To achive compression more common symbols should have shorter codes.
Encoding is a process of converting data written using given alphabet into a binary representation. The process of reconstructing data from binary representation is called decoding.

For introduction to Huffman codes refer to Wikipedia.

Properties of Huffman codes:

• Prefix free i.e. no code is a prefix of another code
• Variable-length i.e. different symbols can have codes of different lengths
• Optimal code length

Obvious decoding

The most obvious method to decode the data encoded using prefix codes is based on traversing the binary tree built from these codes. It is well described for example in this article and in Wikipedia.

At the each step the decoding algorithm consumes only one bit of the input by navigating to the left or the right subtree, producing output symbols upon reaching leaf node and jumping back to the root of the tree. This decoding algorithm can be easily implemented:

            var current = root;
            foreach (var bit in GetBitsFrom(encodedMessage))
            {
              current = bit ? current.right : current.left;
              if (IsLeafNode(current))
              {
                 yield current.Symbol;
                 current = root;
              }
            }
                      

Alternative decoding method

The approach presented here is based on the binary search. On each step, it will decode one input symbol. The algorithm should first preprocess codes. This preprocessing step is done once. Lets assume that each code is less than 32 bits i.e. it will fit in a primitive unsigned integer type. For each code preprocessing step generates two numbers a left-aligned integer code C and a mask M. For example, given the code 11001010111 it should produce the following numbers:

• 1100 1010 111 - input code, length 11 bits.
• 1100 1010 1110 0000 ... 0000 - C the left-aligned integer code (32 bits).
• 1111 1111 1110 0000 ... 0000 - M the mask, 11 significant bits set to 1, the rest are 0.

• Ss - array of symbols, chars.
• Ls - array of code lengths, unsigned integers.
• Cs - array of left-aligned codes, unsigned integers.
• Ms - array of masks, unsigned integers.

Initial step. Construct unsigned integer E from the first 32 bits of the input. Next, perform a binary search over Cs using the mask for comparison. For a valid input the match should always be found at some position i such that: Cs[i] == (E & Ms[i]). This means a symbol Ss[i] is decoded. Next, Ls[i] bits should be removed from E. Technically this means, E should be shifted to the left by Ls[i] bits. And finally, the next Ls[i] bits from the input can be added to E. The algorithm then should continue to the binary search step untill all bits from the input are consumed.

The following code implements presented algorithm: VarLenCharEncoding.cs

This methods works for any prefix-free encoding scheme. Instead of unsigned integers, other primitive integral types can be used if the longest code fits into it.

Consider the following example. Huffman tree and corresponding symbol codes are given below:

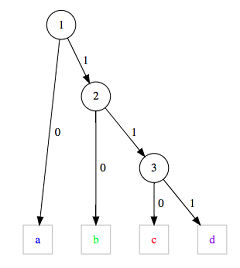
• a -> 0
• b -> 10
• c -> 110
• d -> 111

• Start from the root, node with label 1
• The first bit is one, select the right node with label 2
• The second bit is zero, select the left node
• Selected node is a leaf node, output symbol b
• Jump to the root
• Next bit is zero, select the left node
• Selected node is a leaf node, output symbol a
• Jump to the root
• Next bit is again zero, select the left node
• Selected node is a leaf node, output symbol a
• Jump to the root
• Next bit is one, select the right node with a label 2
• Next bit is one, select the right node with a label 3
• Next bit is one, select the right node
• Selected node is a leaf node, output symbol d
• Jump to the root

• Ss = [a, b, c, d]
• Ls = [1, 2, 3, 3]
• Cs = [0, 8,12,14] in binary form [0000, 1000, 1100, 1110]
• Ms = [8,12,14,14] in binary form [1000, 1100, 1110, 1110]

• E = 8 (10 0 0), rest = (111)
• Binary search, start at (left + right)/2 = (0+4)/2 = 2
• Cs[2] == 12, (E & Ms[2]) == 8, right = 2
Binary search, next (left + right)/2 = (0+2)/2 = 1
Cs[1] == 8, (E & Ms[1]) == 8, match
Output b
• E = (E << Ls[1]) = (8 << 2) = 0
• E = (E | bit1 << 1 | bit2 ) = 0 | 2 | 1 = 3 (0 0 11), rest = (1)
Binary search, start at (left + right)/2 = (0+4)/2 = 2
Cs[2] == 12, (E & Ms[2]) == 2, right = 2
Binary search, next (left + right)/2 = (0+2)/2 = 1
Cs[1] == 8, (E & Ms[1]) == 0, right = 1
Binary search, next (left + right)/2 = (0+1)/2 = 0
Cs[0] == 0, (E & Ms[0]) == 0, match
• Output a
• E = (E << Ls[0]) = (3 << 1) = 6
• E = (E | bit1 ) = 6 | 1 = 7 (0 111), rest = ()
Binary search, start at (left + right)/2 = (0+4)/2 = 2
Cs[2] == 12, (E & Ms[2]) == 6, right = 2
Binary search, next (left + right)/2 = (0+2)/2 = 1
Cs[1] == 8, (E & Ms[1]) == 4, right = 1
Binary search, next (left + right)/2 = (0+1)/2 = 0
Cs[0] == 0, (E & Ms[0]) == 0, match
• Output a
• E = (E << Ls[0]) = (7 << 1) = 14
• No more input, E = 14 (111), rest = ()
Binary search, start at (left + right)/2 = (0+4)/2 = 2
Cs[2] == 12, (E & Ms[2]) == 14, left = 3
Binary search, next (left + right)/2 = (3+4)/2 = 3
Cs[3] == 14, (E & Ms[3]) == 14, match
• Output d