Solution of Facebook Hacker Cup 2012 problem – Squished status
Some engineers got tired of dealing with all the different ways of encoding status messages, so they decided to invent their own. In their new scheme, an encoded status message consists of a sequence of integers representing the characters in the message, separated by spaces. Each integer is between 1 and M, inclusive. The integers do not have leading zeroes. Unfortunately they decided to compress the encoded status messages by removing all the spaces!
Your task is to figure out how many different encoded status messages a given compressed status message could have originally been. Because this number can be very large, you should return the answer modulo 4207849484 (0xfaceb00c in hex).
For example, if the compressed status message is “12″ it might have originally been “1 2″, or it might have originally been “12″. The compressed status messages are between 1 and 1000 characters long, inclusive. Due to database corruption, a compressed status may contain sequences of digits that could not result from removing the spaces in an encoded status message.
Input
The input begins with a single integer, N, the number of compressed status messages you must analyze. This will be followed by N compressed status messages, each consisting of an integer M, the highest character code for that database, then the compressed status message, which will be a string of digits each in the range ’0′ to ’9′, inclusive. All tokens in the input will be separated by some whitespace.
Output
For each of the test cases numbered in order from 1 to N, output “Case #i: ” followed by a single integer containing the number of different encoded status messages that could be represented by the corresponding compressed sequence modulo 4207849484. If none are possible, output a 0.
Constraints
5 <= N <= 25
2 <= M <= 255
1 <= length of encoded status <= 1000
Example input
5
12
12
255
219
30
1234321
2
101
70 8675309
Example output
Case #1: 2
Case #2: 4
Case #3: 6
Case #4: 0
Case #5: 2
Preliminaries
Lets assume that there is a routine which splits input string into a sequence of the smallest valid numbers. Zero and numbers greater than max value M are invalid. Consider following examples:
Input: M=2, S=101
Output: L= {} – Input is invalid
Input: M=11, S=101
Output: L= {10, 1}
Input: M=124, S=18143
Output: L= {1, 8, 1, 4, 3}
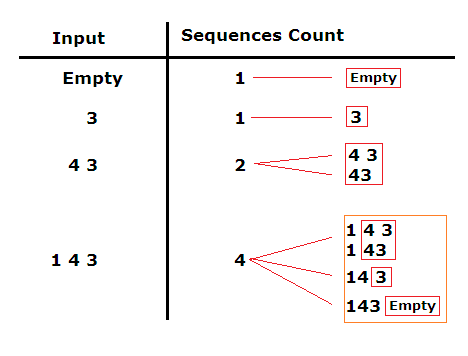
Now lets concentrate on solving the following problem. Given a sequence of numbers - L, count all possible sequences that could be constructed from original sequence by combining consecutive numbers, such that obtained number is less than maximum value M.
Example, given M = 181 and L={1, 4, 3} we can construct 4 sequences:
- {1, 4, 3} – original sequence is valid
- {1, 43}
- {14, 3}
- {143}
Naïve approach
An obvious solution is to perform exhaustive search and construct all such sequences. The algorithm is as simple as:
- If sequence contains one value return 1.
- Put count = 0
- For each number in the sequence
- Try to combine it with the next number (if it exists).
- If combination is not possible proceed to the next number.
- Otherwise replace two consecutive numbers with combined value, recursively call this routine with modified sequence, put count = 1 + returned value, restore sequence. Proceed to the next number
- Try to combine it with the next number (if it exists).
No surprise this approach will only work for small sequences ~ 15-20 numbers.
But we can do better, by figuring out recurrent formula for possible number of valid sequences.
Recurrent formula
Let’s imagine that we calculated the number of different sequences S(L) for input of n numbers:
S({x1, x2, …, xn} ) = Sn
What will happen if we add another number xn+1? We might notice that:
S({x1, x2, …, xn, xn+1 } ) = S({x1, x2, …, xn})+ S({x1, x2, …, (xn xn+1)})
+ S({x1, x2, …, (xn-1 xn xn+1)}).
S({x1, x2, …, (xn xn+1)}) = S({x1, x2, …, xn-1}).
S({x1, x2, …, (xn-1 xn xn+1)}) = S({x1, x2, …, xn-2}).
The structure of solutions is shown on this illustration:
Links
Code